table of contents
This is a short post to collect some context and notes about generative modeling and to try the experiment of generating images of cats using KPN denoising in pixel space. This is not a comprehensive technical report, but I was just curious to see if I could get anything out of this approach.
Diffusion models typically work in latent space for image generation. [3] Using direct noise prediction, but I wanted to see how well it works in pixel space Using a KPN bilateral filter and directly predicting a low rank target rather than predicting the noise velocity on top of it, this allows for a lower rank constraint that can help with generalization and reduce the capacity of the network compared to those that need to predict full rank off-manifold targets.
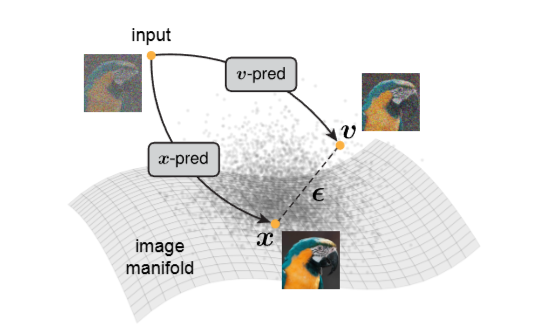
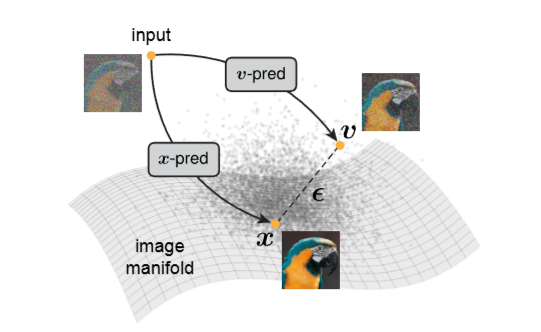
Source [4]
So what I am trying is iterative interpolation to low rank manifolds using a denoising kernel operator.
The advantage of KPN is that it has really good regularization bias as well as behaves well after quantization which makes it suitable for deployment on edge devices. Furthermore KPN filters can be efficiently implemented on GPUs.
The model is trained on 64×64 images of cats from Cats Face 64×64 (for the generative model), using an architecture with a stack of 8×8 patch transformers and upscaling convolutions in the backbone that drive a KPN filtering network for denoising. The training process involves exposing the image to Gaussian noise so that information is gradually lost and then training the model to predict the original image from that noisy input using L2 and LPIPS. [7],
The problem with bilateral filters is that they compute the output as a convex combination of the input pixels, making it hard to create information that is not already present in the input. To mitigate this, I use a separate low capacity network to predict color drift (bias) which is added after the filtering stage, the architecture of the drift prediction model is very simple which guarantees that it does not do the heavy lifting. Also, I do not normalize the binomial weights to sum to 1 and do not allow them to be negative with tanh(x) activation. This makes the filtering non-convex and helps introduce new colors and details that were destroyed by the noise process.
To filter the network I use a simplified version of the partition pyramid from Neural Partitioning Pyramid to denoise the Monte Carlo rendering:
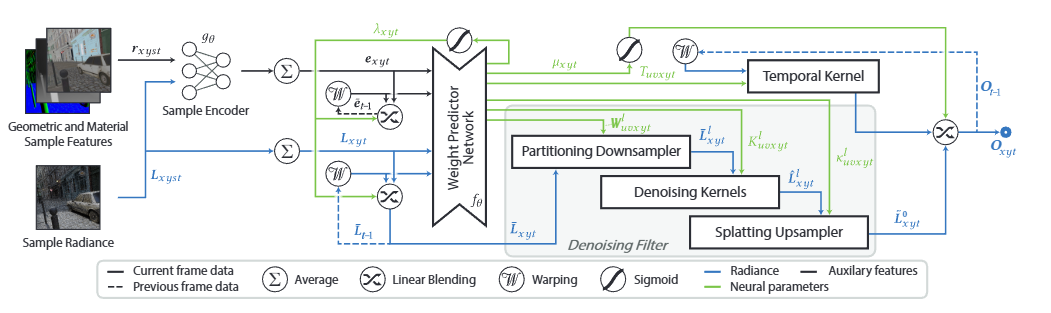
Bartlomiej Wronski: Procedural Kernel Networks with some tips to make it more efficient:

Such as using low rank precision matrix Gaussian parametrization to reduce the number of parameters required for kernel prediction.
To filter the network I use a 5×5 spatial kernel, followed by downsampling by 2×2 average pooling, and for upsampling I use a low rank Gaussian 5×5 with sigmoid LRP with skips, so it’s like a unet but for images.
To predict color drift I use a small U-net that works on RGB 64×64 source images and predicts the channel offset per pixel added after the filtering step.
The idea is that color drift with potentially less detail can be predicted more easily than the entire image, as it only needs to capture the low frequency components of the image. And it will run at full accuracy which helps with color fidelity while KPN filtering can be quantified more aggressively.
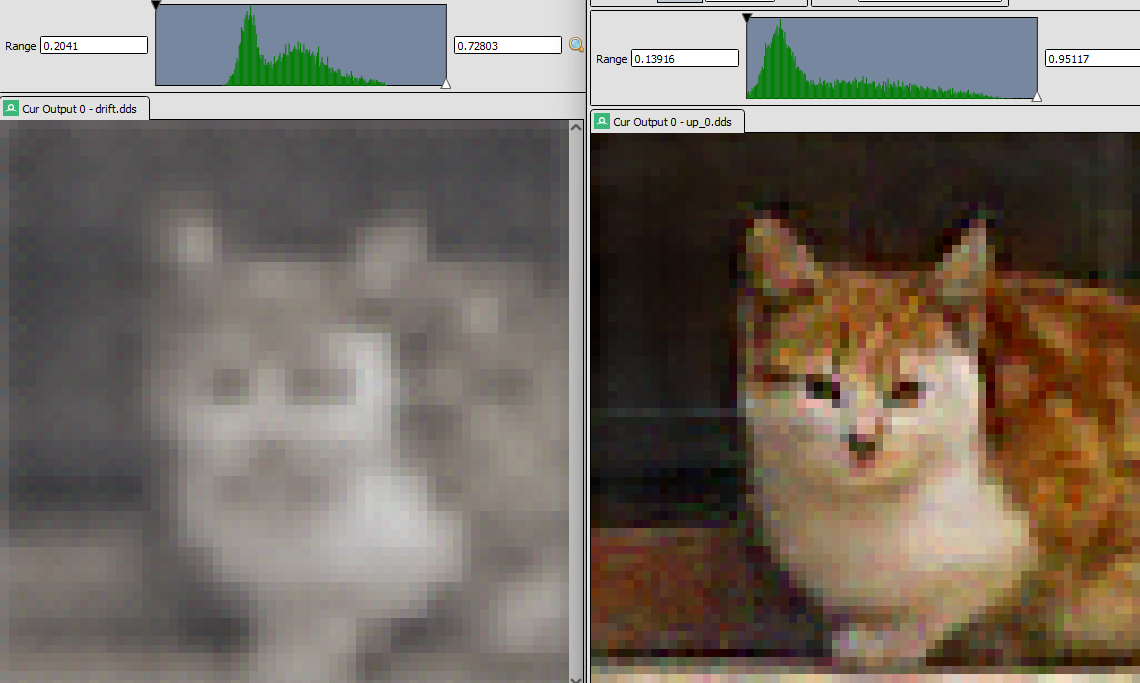
Drift on the left, KPN filtered output on the right.
Here are some generated samples after training for about 5k epochs. Nothing impressive, but interesting as a ‘proof of concept’.


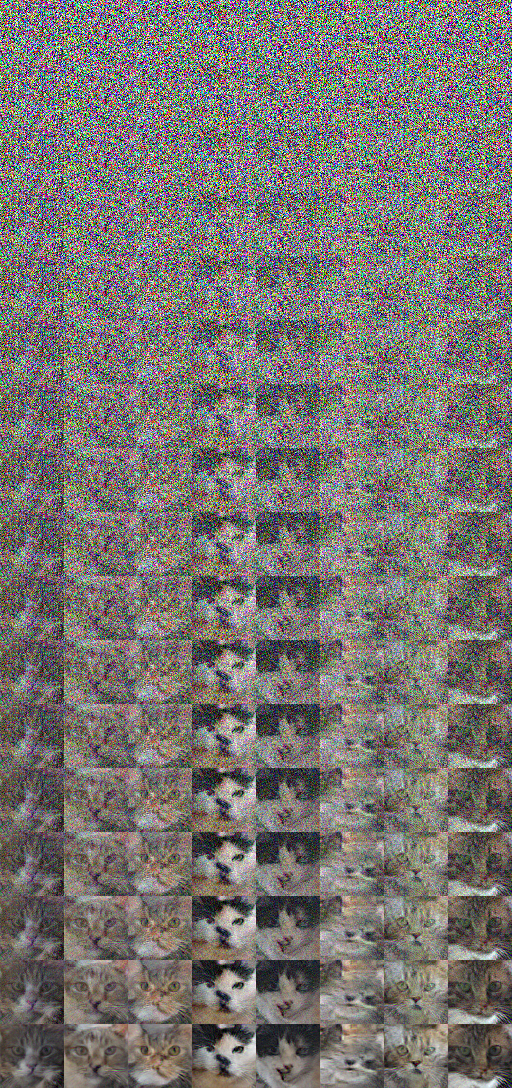
code
[1]Understand Diffusion Models with VAE
[2]Variational Autoencoders and Diffusion Models
[3]Generative modeling in latent space
[4]Back to Basics: Let’s Denoise Generative Models
[5]Neural Segmentation Pyramid for denoising Monte Carlo renderings
[6]Bartlomiej Wronski: Procedural Kernel Network
[7]Unreasonable effectiveness of deep features as a perceptual metric.
<a href